CONTENTS

Utility Functions

pymatting.boxfilter

🔗

Signature

boxfilter(src, radius=3, mode="same")

Function Description

Computes the boxfilter (uniform blur, i.e. blur with kernel np.ones(radius, radius)) of an input image.
Depending on the mode, the input image of size \((h, w)\) is either of shape
  • \((h - 2 r, w - 2 r)\) in case of 'valid' mode
  • \((h, w)\) in case of 'same' mode
  • \((h + 2 r, w + 2 r)\) in case of 'full' mode

Parameters

  • src (numpy.ndarray)
      Input image having either shape \(h \times w \times d\) or \(h \times w\)
  • radius (int)
      Radius of boxfilter, defaults to \(3\)
  • mode (str)
      One of 'valid', 'same' or 'full', defaults to 'same'

Returns

  • dst (numpy.ndarray)
      Blurred image

Example

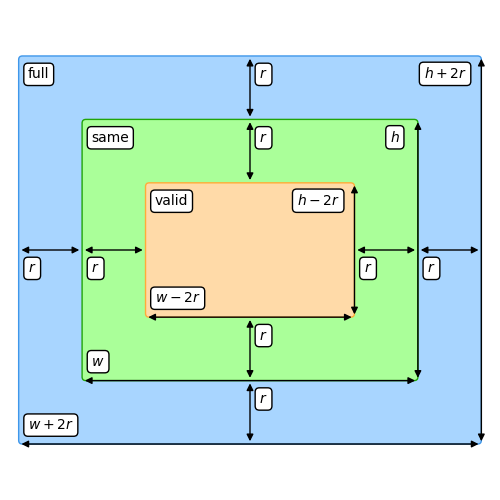
>>> from pymatting import * >>> import numpy as np >>> boxfilter(np.eye(5), radius=2, mode="valid") array([[5.]]) >>> boxfilter(np.eye(5), radius=2, mode="same") array([[3., 3., 3., 2., 1.], [3., 4., 4., 3., 2.], [3., 4., 5., 4., 3.], [2., 3., 4., 4., 3.], [1., 2., 3., 3., 3.]]) >>> boxfilter(np.eye(5), radius=2, mode="full") array([[1., 1., 1., 1., 1., 0., 0., 0., 0.], [1., 2., 2., 2., 2., 1., 0., 0., 0.], [1., 2., 3., 3., 3., 2., 1., 0., 0.], [1., 2., 3., 4., 4., 3., 2., 1., 0.], [1., 2., 3., 4., 5., 4., 3., 2., 1.], [0., 1., 2., 3., 4., 4., 3., 2., 1.], [0., 0., 1., 2., 3., 3., 3., 2., 1.], [0., 0., 0., 1., 2., 2., 2., 2., 1.], [0., 0., 0., 0., 1., 1., 1., 1., 1.]])

pymatting.knn

🔗

Signature

knn(data_points, query_points, k)

Function Description

Find k nearest neighbors in a data set. The implementation currently only supports data type np.float32.

Parameters

  • data_points (numpy.ndarray (of type `np.float32`))
      Dataset with shape \(n \times d\), where \(n\) is the number of data points in the data set and \(d\) is the dimension of each data point
  • query_points (numpy.ndarray (of type `np.float32`))
      Data points for which the next neighbours should be calculated
  • k (int)
      Number of neighbors to find

Returns

  • distances (numpy.ndarray)
      Distances to the neighbors
  • indices (numpy.ndarray)
      Indices of the k nearest neighbors in original data array

Example

>>> from pymatting import * >>> import numpy as np >>> data_set = np.random.randn(100, 2) >>> knn(data_set.astype(np.float32), np.array([[0.5,0.5]], dtype=np.float32), k=2) (array([[0.16233477, 0.25393516]], dtype=float32), array([[25, 17]]))

pymatting.KDTree.__init__

🔗

Signature

__init__(self, data_points, min_leaf_size=8)

Function Description

Constructs a KDTree for given data points. The implementation currently only supports data type np.float32.

Parameters

  • data_points (numpy.ndarray (of type `np.float32`))
      Dataset with shape \(n \times d\), where \(n\) is the number of data points in the data set and \(d\) is the dimension of each data point
  • min_leaf_size (int)
      Minimum number of nodes in a leaf, defaults to 8

Example

>>> from pymatting import * >>> import numpy as np >>> data_set = np.random.randn(100, 2) >>> tree = KDTree(data_set.astype(np.float32))

pymatting.KDTree.query

🔗

Signature

query(self, query_points, k)

Function Description

Query the tree

Parameters

  • query_points (numpy.ndarray (of type `np.float32`))
      Data points for which the next neighbours should be calculated
  • k (int)
      Number of neighbors to find

Returns

  • distances (numpy.ndarray)
      Distances to the neighbors
  • indices (numpy.ndarray)
      Indices of the k nearest neighbors in original data array

Example

>>> from pymatting import * >>> import numpy as np >>> data_set = np.random.randn(100, 2) >>> tree = KDTree(data_set.astype(np.float32)) >>> tree.query(np.array([[0.5,0.5]], dtype=np.float32), k=3) (array([[0.14234178, 0.15879704, 0.26760164]], dtype=float32), array([[29, 21, 20]]))

pymatting.Timer.__init__

🔗

Signature

__init__(self)

Function Description

Starts a timer

pymatting.Timer.stop

🔗

Signature

stop(self, message=None)

Function Description

Return and print time since last stop-call or initialization. Also print elapsed time if message is provided.

Parameters

  • message (str)
      Message to print in front of passed seconds

Example

>>> from pymatting import * >>> t = Timer() >>> t.stop() 2.6157200919999966 >>> t = Timer() >>> t.stop('Test') Test - 11.654551 seconds 11.654551381000001

pymatting.apply_to_channels

🔗

Signature

apply_to_channels(single_channel_func)

Function Description

Creates a new function which operates on each channel

Parameters

  • single_channel_func (function)
      Function that acts on a single color channel

Returns

  • channel_func (function)
      The same function that operates on all color channels

Example

>>> from pymatting import * >>> import numpy as np >>> from scipy.signal import convolve2d >>> single_channel_fun = lambda x: convolve2d(x, np.ones((3, 3)), 'valid') >>> multi_channel_fun = apply_to_channels(single_channel_fun) >>> I = np.random.rand(480, 320, 3) >>> multi_channel_fun(I).shape (478, 318, 3)

pymatting.vec_vec_dot

🔗

Signature

vec_vec_dot(a, b)

Function Description

Computes the dot product of two vectors.

Parameters

  • a (numpy.ndarray)
      First vector (if np.ndim(a) > 1 the function calculates the product for the two last axes)
  • b (numpy.ndarray)
      Second vector (if np.ndim(b) > 1 the function calculates the product for the two last axes)

Returns

  • product (scalar)
      Dot product of a and b

Example

>>> import numpy as np >>> from pymatting import * >>> a = np.ones(2) >>> b = np.ones(2) >>> vec_vec_dot(a,b) 2.0

pymatting.mat_vec_dot

🔗

Signature

mat_vec_dot(A, b)

Function Description

Calculates the matrix vector product for two arrays.

Parameters

  • A (numpy.ndarray)
      Matrix (if np.ndim(A) > 2 the function calculates the product for the two last axes)
  • b (numpy.ndarray)
      Vector (if np.ndim(b) > 1 the function calculates the product for the two last axes)

Returns

  • product (numpy.ndarray)
      Matrix vector product of both arrays

Example

>>> import numpy as np >>> from pymatting import * >>> A = np.eye(2) >>> b = np.ones(2) >>> mat_vec_dot(A,b) array([1., 1.])

pymatting.vec_vec_outer

🔗

Signature

vec_vec_outer(a, b)

Function Description

Computes the outer product of two vectors
a: numpy.ndarray First vector (if np.ndim(b) > 1 the function calculates the product for the two last axes) b: numpy.ndarray Second vector (if np.ndim(b) > 1 the function calculates the product for the two last axes)

Returns

  • product (numpy.ndarray)
      Outer product of a and b as numpy.ndarray

Example

>>> import numpy as np >>> from pymatting import * >>> a = np.arange(1,3) >>> b = np.arange(1,3) >>> vec_vec_outer(a,b) array([[1, 2], [2, 4]])

pymatting.fix_trimap

🔗

Signature

fix_trimap( trimap, lower_threshold=0.1, upper_threshold=0.9)

Function Description

Fixes broken trimap \(T\) by thresholding the values
$$ T^{\text{fixed}}_{ij}= \begin{cases} 0,&\text{if } T_{ij}<\text{lower\_threshold}\\ 1,&\text{if }T_{ij}>\text{upper\_threshold}\\ 0.5, &\text{otherwise}.\\ \end{cases} $$

Parameters

  • trimap (numpy.ndarray)
      Possibly broken trimap
  • lower_threshold (float)
      Threshold used to determine background pixels, defaults to 0.1
  • upper_threshold (float)
      Threshold used to determine foreground pixels, defaults to 0.9

Returns

  • fixed_trimap (numpy.ndarray)
      Trimap having values in \(\{0, 0.5, 1\}\)

Example

>>> from pymatting import * >>> import numpy as np >>> trimap = np.array([0,0.1, 0.4, 0.9, 1]) >>> fix_trimap(trimap, 0.2, 0.8) array([0. , 0. , 0.5, 1. , 1. ])

pymatting.isiterable

🔗

Signature

isiterable(obj)

Function Description

Checks if an object is iterable

Parameters

  • obj (object)
      Object to check

Returns

  • is_iterable (bool)
      Boolean variable indicating whether the object is iterable

Example

>>> from pymatting import * >>> l = [] >>> isiterable(l) True

pymatting.load_image

🔗

Signature

load_image( path, mode=None, size=None, resample="box")

Function Description

This function can be used to load an image from a file.

Parameters

  • path (str)
      Path of image to load.
  • mode (str)
      Can be "GRAY", "RGB" or something else (see PIL.convert())

Returns

  • image (numpy.ndarray)
      Loaded image

pymatting.save_image

🔗

Signature

save_image(path, image, make_directory=True)

Function Description

Given a path, save an image there.

Parameters

  • path (str)
      Where to save the image.
  • image (numpy.ndarray, dtype in [np.uint8, np.float32, np.float64])
      Image to save. Images of float dtypes should be in range [0, 1]. Images of uint8 dtype should be in range [0, 255]
  • make_directory (bool)
      Whether to create the directories needed for the image path.

pymatting.to_rgb8

🔗

Signature

to_rgb8(image)

Function Description

Convertes an image to rgb8 color space

Parameters

  • image (numpy.ndarray)
      Image to convert

Returns

  • image (numpy.ndarray)
      Converted image with same height and width as input image but with three color channels

Example

>>> from pymatting import * >>> import numpy as np >>> I = np.eye(2) >>> to_rgb8(I) array([[[255, 255, 255], [ 0, 0, 0]], [[ 0, 0, 0], [255, 255, 255]]], dtype=uint8)

pymatting.make_grid

🔗

Signature

make_grid(images, nx=None, ny=None, dtype=None)

Function Description

Plots a grid of images.

Parameters

  • images (list of numpy.ndarray)
      List of images to plot
  • nx (int)
      Number of rows
  • ny (int)
      Number of columns
  • dtype (type)
      Data type of output array

Returns

  • grid (numpy.ndarray)
      Grid of images with datatype dtype

pymatting.show_images

🔗

Signature

show_images(images)

Function Description

Plot grid of images.

Parameters

  • images (list of numpy.ndarray)
      List of images to plot
  • height (int, matrix)
      Height in pixels the output grid, defaults to 512

pymatting.trimap_split

🔗

Signature

trimap_split( trimap, flatten=True, bg_threshold=0.1, fg_threshold=0.9)

Function Description

This function splits the trimap into foreground pixels, background pixels, and unknown pixels.
Foreground pixels are pixels where the trimap has values larger than or equal to fg_threshold (default: 0.9). Background pixels are pixels where the trimap has values smaller than or equal to bg_threshold (default: 0.1). Pixels with other values are assumed to be unknown.

Parameters

  • trimap (numpy.ndarray)
      Trimap with shape \(h \times w\)
  • flatten (bool)
      If true np.flatten is called on the trimap

Returns

  • is_fg (numpy.ndarray)
      Boolean array indicating which pixel belongs to the foreground
  • is_bg (numpy.ndarray)
      Boolean array indicating which pixel belongs to the background
  • is_known (numpy.ndarray)
      Boolean array indicating which pixel is known
  • is_unknown (numpy.ndarray)
      Boolean array indicating which pixel is unknown
  • bg_threshold (float)
      Pixels with smaller trimap values will be considered background.
  • fg_threshold (float)
      Pixels with larger trimap values will be considered foreground.

Example

>>> import numpy as np >>> from pymatting import * >>> trimap = np.array([[1,0],[0.5,0.2]]) >>> is_fg, is_bg, is_known, is_unknown = trimap_split(trimap) >>> is_fg array([ True, False, False, False]) >>> is_bg array([False, True, False, False]) >>> is_known array([ True, True, False, False]) >>> is_unknown array([False, False, True, True])

pymatting.sanity_check_image

🔗

Signature

sanity_check_image(image)

Function Description

Performs a sanity check for input images. Image values should be in the range [0, 1], the dtype should be np.float32 or np.float64 and the image shape should be (?, ?, 3).

Parameters

  • image (numpy.ndarray)
      Image with shape \(h \times w \times 3\)

Example

>>> import numpy as np >>> from pymatting import check_image >>> image = (np.random.randn(64, 64, 2) * 255).astype(np.int32) >>> sanity_check_image(image) __main__:1: UserWarning: Expected RGB image of shape (?, ?, 3), but image.shape is (64, 64, 2). __main__:1: UserWarning: Image values should be in [0, 1], but image.min() is -933. __main__:1: UserWarning: Image values should be in [0, 1], but image.max() is 999. __main__:1: UserWarning: Unexpected image.dtype int32. Are you sure that you do not want to use np.float32 or np.float64 instead?

pymatting.blend

🔗

Signature

blend(foreground, background, alpha)

Function Description

This function composes a new image for given foreground image, background image and alpha matte.
This is done by applying the composition equation
$$ I = \alpha F + (1-\alpha)B. $$

Parameters

  • foreground (numpy.ndarray)
      Foreground image
  • background (numpy.ndarray)
      Background image
  • alpha (numpy.ndarray)
      Alpha matte

Returns

  • image (numpy.ndarray)
      Composed image as numpy.ndarray

Example

>>> from pymatting import * >>> foreground = load_image("data/lemur/lemur_foreground.png", "RGB") >>> background = load_image("data/lemur/beach.png", "RGB") >>> alpha = load_image("data/lemur/lemur_alpha.png", "GRAY") >>> I = blend(foreground, background, alpha)

pymatting.stack_images

🔗

Signature

stack_images()

Function Description

This function stacks images along the third axis. This is useful for combining e.g. rgb color channels or color and alpha channels.

Parameters

    • images: numpy.ndarray
    Images to be stacked.

    Returns

    • image (numpy.ndarray)
        Stacked images as numpy.ndarray

    Example

    >>> from pymatting.util.util import stack_images >>> import numpy as np >>> I = stack_images(np.random.rand(4,5,3), np.random.rand(4,5,3)) >>> I.shape (4, 5, 6)

    pymatting.row_sum

    🔗

    Signature

    row_sum(A)

    Function Description

    Calculate the sum of each row of a matrix

    Parameters

    • A (np.ndarray or scipy.sparse.spmatrix)
        Matrix to sum rows of

    Returns

    • row_sums (np.ndarray)
        Vector of summed rows

    Example

    >>> from pymatting import * >>> import numpy as np >>> A = np.random.rand(2,2) >>> A array([[0.62750946, 0.12917617], [0.8599449 , 0.5777254 ]]) >>> row_sum(A) array([0.75668563, 1.4376703 ])

    pymatting.normalize_rows

    🔗

    Signature

    normalize_rows(A, threshold=0.0)

    Function Description

    Normalize the rows of a matrix
    Rows with sum below threshold are left as-is.

    Parameters

    • A (scipy.sparse.spmatrix)
        Matrix to normalize
    • threshold (float)
        Threshold to avoid division by zero

    Returns

    • A (scipy.sparse.spmatrix)
        Matrix with normalized rows

    Example

    >>> from pymatting import * >>> import numpy as np >>> A = np.arange(4).reshape(2,2) >>> normalize_rows(A) array([[0. , 1. ], [0.4, 0.6]])

    pymatting.grid_coordinates

    🔗

    Signature

    grid_coordinates(width, height, flatten=False)

    Function Description

    Calculates image pixel coordinates for an image with a specified shape

    Parameters

    • width (int)
        Width of the input image
    • height (int)
        Height of the input image
    • flatten (bool)
        Whether the array containing the coordinates should be flattened or not, defaults to False

    Returns

    • x (numpy.ndarray)
        x coordinates
    • y (numpy.ndarray)
        y coordinates

    Example

    >>> from pymatting import * >>> x, y = grid_coordinates(2,2) >>> x array([[0, 1], [0, 1]]) >>> y array([[0, 0], [1, 1]])

    pymatting.sparse_conv_matrix_with_offsets

    🔗

    Signature

    sparse_conv_matrix_with_offsets( width, height, kernel, dx, dy)

    Function Description

    Calculates a convolution matrix that can be applied to a vectorized image
    Additionally, this function allows to specify which pixels should be used for the convoltion, i.e.
    $$ \left(I * K\right)_{ij} = \sum_k K_k I_{i+{\Delta_y}_k,j+{\Delta_y}_k}, $$
    where \(K\) is the flattened convolution kernel.

    Parameters

    • width (int)
        Width of the input image
    • height (int)
        Height of the input image
    • kernel (numpy.ndarray)
        Convolutional kernel
    • dx (numpy.ndarray)
        Offset in x direction
    • dy (nunpy.ndarray)
        Offset in y direction

    Returns

    • M (scipy.sparse.csr_matrix)
        Convolution matrix

    pymatting.sparse_conv_matrix

    🔗

    Signature

    sparse_conv_matrix(width, height, kernel)

    Function Description

    Calculates a convolution matrix that can be applied to a vectorized image

    Parameters

    • width (int)
        Width of the input image
    • height (int)
        Height of the input image
    • kernel (numpy.ndarray)
        Convolutional kernel

    Returns

    • M (scipy.sparse.csr_matrix)
        Convolution matrix

    Example

    >>> from pymatting import * >>> import numpy as np >>> sparse_conv_matrix(3,3,np.ones((3,3))) <9x9 sparse matrix of type '<class 'numpy.float64'>' with 49 stored elements in Compressed Sparse Row format>

    pymatting.weights_to_laplacian

    🔗

    Signature

    weights_to_laplacian( W, normalize=True, regularization=0.0)

    Function Description

    Calculates the random walk normalized Laplacian matrix from the weight matrix

    Parameters

    • W (numpy.ndarray)
        Array of weights
    • normalize (bool)
        Whether the rows of W should be normalized to 1, defaults to True
    • regularization (float)
        Regularization strength, defaults to 0, i.e. no regularizaion

    Returns

    • L (scipy.sparse.spmatrix)
        Laplacian matrix

    Example

    >>> from pymatting import * >>> import numpy as np >>> weights_to_laplacian(np.ones((4,4))) matrix([[ 0.75, -0.25, -0.25, -0.25], [-0.25, 0.75, -0.25, -0.25], [-0.25, -0.25, 0.75, -0.25], [-0.25, -0.25, -0.25, 0.75]])

    pymatting.normalize

    🔗

    Signature

    normalize(values)

    Function Description

    Normalizes an array such that all values are between 0 and 1

    Parameters

    • values (numpy.ndarray)
        Array to normalize

    Returns

    • result (numpy.ndarray)
        Normalized array

    Example

    >>> from pymatting import * >>> import numpy as np >>> normalize(np.array([0, 1, 3, 10])) array([0. , 0.1, 0.3, 1. ])

    pymatting.div_round_up

    🔗

    Signature

    div_round_up(x, n)

    Function Description

    Divides a number x by another integer n and rounds up the result

    Parameters

    • x (int)
        Numerator
    • n (int)
        Denominator

    Returns

    • result (int)
        Result

    Example

    >>> from pymatting import * >>> div_round_up(3,2) 2